こんばんは。
今日は建築士試験の構造分野から、塑性ヒンジなどのお話。主に鉄骨系の骨組みの崩壊状態を調べる上で必須の問題です。
目次
塑性変形とは?
物体に外力が作用して変形が生じている時、外力を取り除くと変形が元に戻るのが弾性変形。それに対して、外力を取り除いても変形が元に戻らないのが塑性変形。
例えば、針金に力を加えて曲げるとき、はじめはちゃんと元に戻ってきますが、曲げ過ぎると元に戻らなくなります。これは針金の変形が弾性限界を超えたということ。また別の例では、透明なプラスティックの板を曲げていくと、曲げ過ぎるとある部分が白く色が変わっていき、変形が元に戻らなくなります。
塑性域に達した後の応力状態
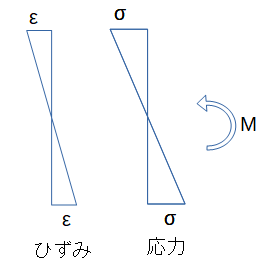
さて、ある完全弾塑性の梁に曲げモーメントが作用した場合の応力を考えます。弾性範囲内では、応力は歪みに比例するので、図のようになります。

歪みが大きくなると、断面の端から弾性限界に達します。そうなると、応力は増えないまま変形だけが進んでいきます。下図のように断面の半分が塑性化した場合、荷重を取り除くと少しだけ変形が元に戻りますが、完全には戻りません。

さらに変形が進み、断面の全部が塑性化した場合、荷重が増えなくても変形がどんどん進んでいってしまいます。この状態が全塑性状態で、この時の曲げモーメントを全塑性モーメントといいます。

全塑性モーメント
全塑性モーメントとは、要するにある梁が崩壊するギリギリの状態で負担できる最大の曲げモーメントということになり、骨組みの終局状態を求める際に重要となってきます。
さて、この全塑性モーメントですが、求めるのは簡単。断面の全てが降伏応力として、モーメントを求めるだけです。
以下のような幅b、高さhの長方形断面の場合、上下それぞれの面積に降伏応力
が作用しており、その偶力の間の距離は
なので、全塑性モーメントMpは、
となります。

この他、H型鋼などでも同様に、全断面が降伏応力に達していると考えて、モーメントを計算するだけです。
塑性断面係数
最後に、塑性断面係数Zpについて。これは、弾性の時の曲げモーメントと応力の関係を繋ぐ断面係数と同じで、以下のように定義されます。
ということで、全塑性モーメントと塑性断面係数についての解説でした。