こんばんは。
梁やラーメンの問題を解くときに、最初に静定か不静定の判別を行う必要があります。判別式にはいくつか種類があるので、解説していきます。
目次
静定とは?
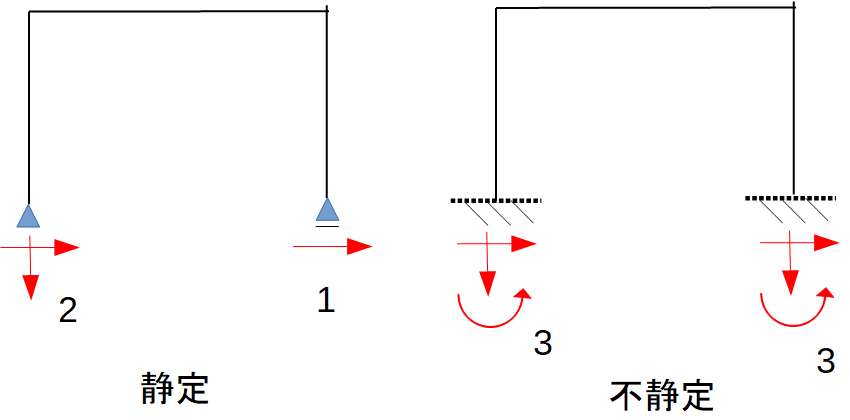
静定構造物とは、力の釣り合いだけで反力を求めることができる構造をいいます。
左の図の場合、未知の反力は3つですので、上下・左右の力の釣り合いとモーメントの釣り合いの3つの条件だけで反力を求めることができます。一方、右の図では、未知の反力が6個となりますので、釣り合い条件だけで反力を求めることができません。(このケースでは、3次の不静定構造になります。)

判別式の色々
さて、もっと複雑な形状の構造の場合、静定・不静定を判別するには、いかの判別式を使うことができます。こちらのサイトに詳しく載っています。
https://shake.tu.chiba-u.jp/lecture/StrMcnI/pdf/StrMcnI_03.pdf
判別式①
反力数n、反力以外の未知の力の数m、自由物体体の数Sを用いる次式がゼロならば静定。

判別式②
反力数n、部材結合力の数m、自由物体体Sの数を用いる次式がゼロならば静定。

判別式③
剛節数r、反力数n、部材数S、全節点数kを用いる次式がゼロならば静定。

分かりやすさで言うと、判別式③がお勧めとのこと。
不静定だったらどうする?
さて、不静定構造とわかった場合、どうやって反力を求めればよいか。基本的には、①端点の拘束を解除して、静定構造に分解する。②静定構造の反力と変位を求める。③適合条件を使って未知数を求める
というのが、一般な解法になります。(具体的な例はまた次の機会に)