中立軸に関する問題は、1級建築士試験でもたまに出題されます。勉強すれば確実に点を取れる問題なので、しっかり理解しておきましょう。
目次
中立軸とは?
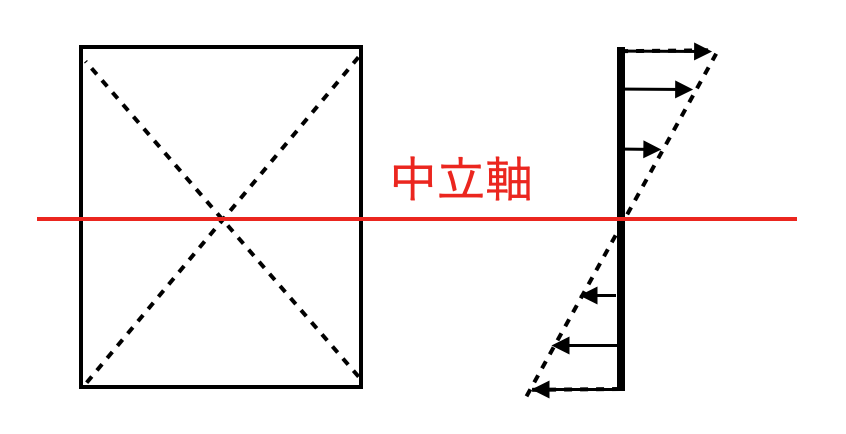
中立軸とは、曲げモーメントが作用したときに、断面のなかで引っ張りも圧縮も生じない位置のことを言います。図心の位置が中立軸となります。
過去問の例
中立軸を求める問題としては、最近では2019年に以下のような出題がありました。断面1次モーメント、全塑性モーメントとの関連での出題です。
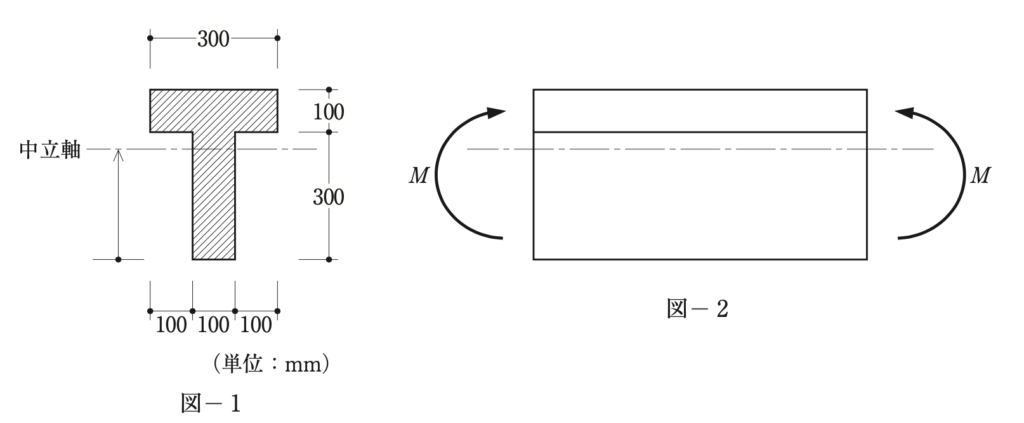
等質で、図-1のような断面形状の部材に、図-2のように断面力として曲げモーメン トMのみが作用している。この断面の降伏開始曲げモーメントをMy、全塑性モーメントをMpとする とき、M≦Myの場合とM =Mpの場合の中立軸の位置の組合せとして、正しいものは、次のうちどれか。ただし、中立軸の位置は断面下縁から測るものとする。(2019年構造(1))
ポイント1:断面1次モーメントと図心位置の関係
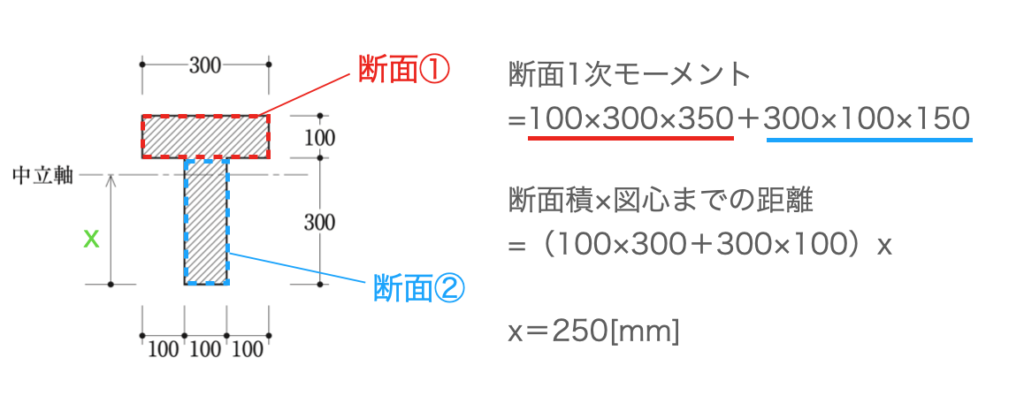
まずは、M≦Myのときの中立軸位置を求めます。これには、断面1次モーメントと図心位置に関する以下の公式を用います。
(公式) 断面1次モーメント=断面積 × 図心までの距離
これをこの問題に適用すると、以下のようになります。
断面1次モーメントと断面積・図心までの距離は基本的な公式なので、しっかり覚えておきましょう。
全塑性モーメントと中立軸位置
断面の全体が降伏応力に到達したときの曲げモーメントを全塑性モーメントと言います。断面が塑性化したときの中立軸位置は、断面が弾性のときの中立軸位置と異なります。
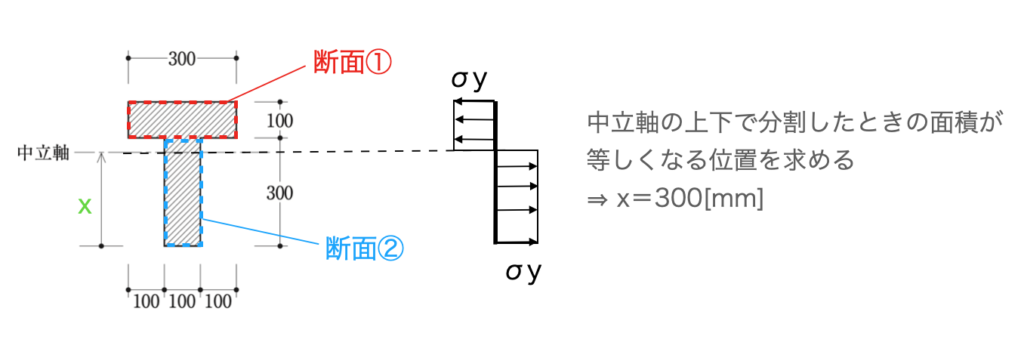
断面の全体が塑性化したときには、断面全体の応力が降伏応力σyで一定としたうえで、中立軸まわりのモーメントの釣り合い式から中立軸位置を求めます。これは、中立軸で断面を分割したときの上下の面積が等しくなる位置を求めることと同じになるので、今回の場合は、以下のようになります。
全塑性モーメントの場合は、断面に生じる応力が全て降伏応力σyで一定になるので、あとは面積だけを考えれば中立軸位置を求める事ができます。


コメント