建築士試験でもたまに出題されるゲルバー梁。その解き方を解説します。
目次
ゲルバー梁とは?
ゲルバー梁とは、梁の途中にヒンジを設けることで、不静定次数を下げて静定構造にしようとする構造をいいます。
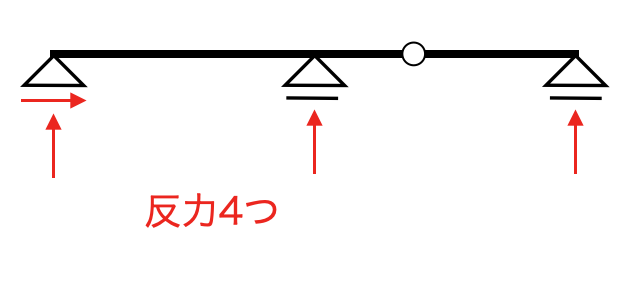
例えば下図のような梁を考えます。左側の梁は不静定構造であり、力の釣り合いだけでは反力を求めることはできません。一方、右側の図はヒンジが加わることにより静定構造となっており、力の釣り合いだけで反力を求めることができます。
ゲルバー梁を見たら、まずは分解してみる
さて、ゲルバー梁に出くわしたらどのように解いていくか。以下のステップで考えれば必ず解けます。
- 梁全体の力の釣り合いを考える。(水平方向、鉛直方向、回転)
- ヒンジ部分で分解する。
- 分解した部分について、モーメント=0とする。
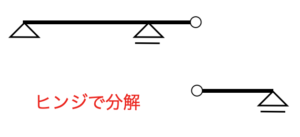
ポイントは2.の分解するというところ。先ほどのゲルバー梁の場合、以下のように分解して2つの梁に分けて考えることになります。
例題
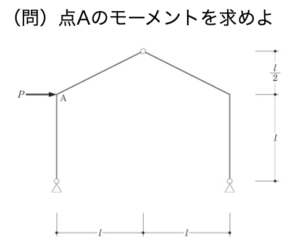
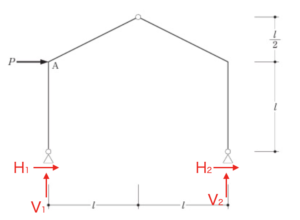
以下の例題で上記の手順を解説します。(2018年構造(3))
①まずは各支点の反力を仮定したうえで、骨組み全体の力の釣り合いを考えます。
(水平方向の力の釣り合い)
$$H_1 + H_2 + P = 0$$
(上下方向の力の釣り合い)
$$V_1+ V_2 = 0$$
(左下の点を中心としたモーメントの釣り合い)
$$ Pl – 2V_2l = 0 $$
この時点では、反力4つに対して条件式が3つしかありませんので、解けません。ここで、ゲルバー梁のヒンジの条件を使用します。
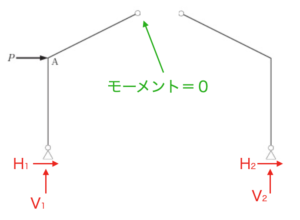
②ヒンジ部分で分解する
ヒンジ部分で分解すると、以下のように2つの梁になります。
③分解した部分について、モーメント=0とする。
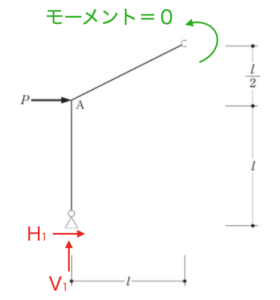
例えば分解した左側について、ヒンジ部分のモーメントは0である条件を入れると、次の条件が成り立ちます。
$$ V_1l – \frac{3}{2}H_1l – \frac{1}{2}Pl = 0 $$
これで、反力4つに対して条件式4つとなり、解くことができるようになりました。4つの式を連立させて解くと、$H_1 = \frac{2}{3}P $ となり、点Aのモーメントは$\frac{2}{3}Pl$となります。
まとめ
- ゲルバー梁はヒンジを設けることで不静定次数を下げる梁
- ゲルバー梁を見たら、まず分解する。
- あとは力の釣り合いから反力を求めるだけ。



コメント